Sigma
Overview
This module calculates the Hammett electronic substituent constant (s, sigma) for selected fragments of a molecule, or substituents.
Interface
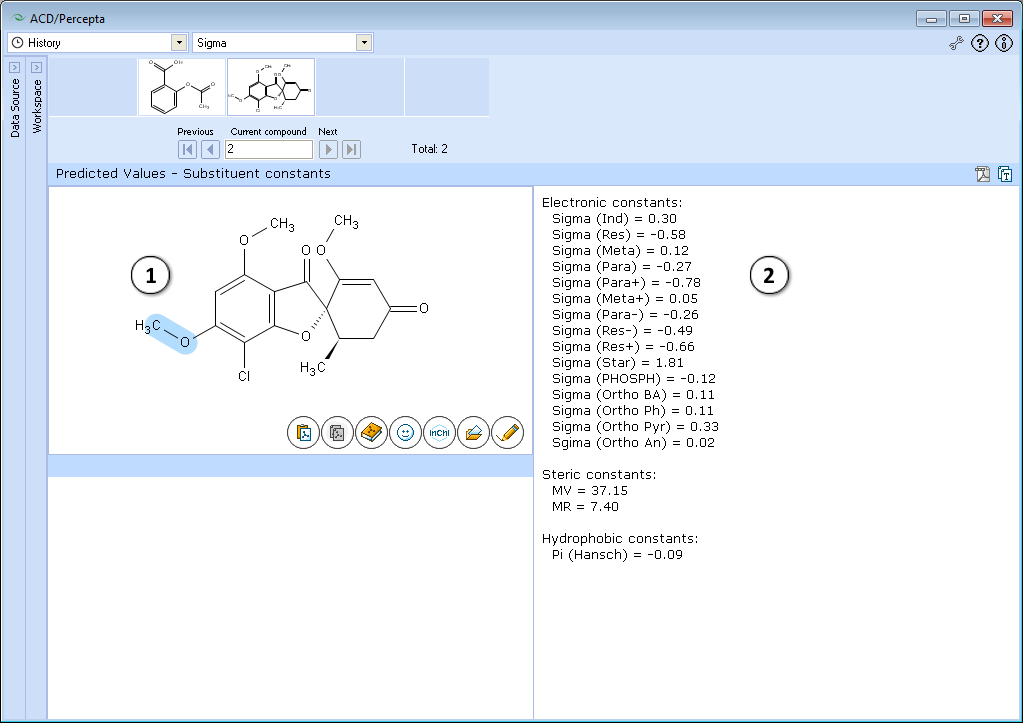
- Click and drag the mouse cursor in the Structure pane to select a fragment of a structure. The selected fragment is highlighted in blue.
- Calculated the Hammett electronic substituent constant (s, sigma) for the selected fragment.
Technical information
Introduction to Sigma
This section will familiarize you with the prediction of the order of reactivity, the meaning of calculated types of sigma with references to the original sources, and the process of sigma calculation.
Predicting the Order of Reactivity
Sigma, and related constants, is an attempt to quantitatively estimate the effect of structure on reactivity. It has been known for decades that the prediction of reactivity is closely related to the molecular structure. Since the 1930s chemists have expressed the ratio of reactions in terms of the Hammett equation [1]. This compares the reaction rates of two compounds, one with a special group attached, and one without.
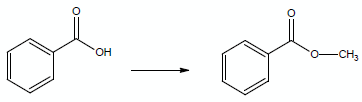
For example, consider the participation of two compounds in a reaction as simple as adding a methyl group to benzoic acid:
If you had a substituent on the ring, say, a tert-butyl group, –C(CH3)3, under certain conditions, the rate of esterification would slow down:

Whereas, if the substituent had been –CF3, under the same conditions, the rate of esterification would speed up:
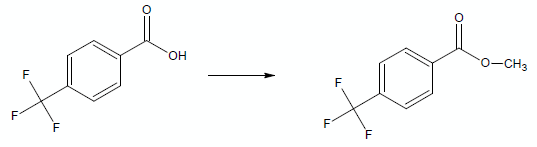
In general, we could say that the order of reaction obeyed the rule:
–C(CH3)3 < no substituent < –CF3
Now, if the reaction changes, can we make a similar prediction about the order of reactivity? In general, yes. (In detail, the order might get flipped so that –C(CH3)3 > no substituent > –CF3 However, the crucial fact remains that the two groups, tert-butyl, and trifluoro methyl, will usually have opposite effects.
Similarly, if we looked at an assortment of different substituents, they could be placed in order, more or less according to how they would affect the rate of reaction.
A simple way to quantify the effects for these groups is to express the ratio of their free energies of reaction; this is the quantity known as sigma, σ.
Variations on a Theme
Over the decades, much research has gone into different types of
- Substituents
- Locations
- Locations within the molecule (e.g., on a ring, on a chain, etc.)
There have been a variety of σ constants proposed, beginning with a distinction between resonance and field effects (inductive) constants, σRes and σI, respectively.
The designations used in ACD/Sigma are extensive:
| Sigma | Meaning |
|---|---|
| σInd | Sigma inductive [2] |
| σRes | Sigma resonance (π-electron delocalization—benzoic acid model) [3] |
| σmeta | Sigma meta for substituent in meta position on aromatic ring (derived from benzoic acids) [4] |
| σpara | Sigma para for substituent in para position on aromatic ring (derived from benzoic acids) [5] |
| σpara+ | Sigma plus para: delocalization +charge (derived from solvolysis of t-cumyl chlorides) [6] |
| σmeta+ | Sigma plus meta. As σpara+ [7] |
| σpara– | Sigma less para: delocalized conjugated negative charge (derived from ionization of phenols or anilines) [8] |
| σRes– | Sigma aniline resonance (π-electron delocalization, aniline model) [9] |
| σRes+ | Sigma plus resonance (π-electron delocalization from t-cumyl chlorides) [10] |
| σ* | Inductive constant of Taft for use in saturated compounds (Taft R.W. Steric Effect in Organic Chemistry. M.S. Newman (Ed.), Wiley, New York, 1956) |
| σPHOSPH | Substituent constant for groups attached directly to a phosphorus atom [11] |
| σortho BA | Sigma ortho (derived from substituted benzoic acid). The same as σmeta or σpara, but for ortho substituents. |
| σortho Ph | Sigma ortho (derived from substituted phenols). The same as σpara–, but for ortho substituents. |
| σortho An | Sigma ortho (derived from substituted anilines). |
| σortho Pyr | Sigma ortho (derived from substituted pyridines). |
Algorithms for Calculating Electronic Substituent Constants
Electronic Effect Transmission Through Skeleton
This is based on the following formula:
σR–G– = σ–G– + ΣzI,R,…–G–∙σI,R,…R– + ΣzI,R,…–G–∙(σIR–∙σRR–)…,
where all σI,R,…R– are substituent R electronic constants (inductive, resonance, etc.) and all zI,R,…sup>–G– are skeleton G transmission constants. The accuracy of the σR–G– calculation is usually better than ±0.05–0.1. The algorithm contains 42 of the most frequently used skeletons G described by 126 such equations:
σI–36, σR–25, σR-–6, σR+–4, σPara–24, σMeta–24, σPhosph–7
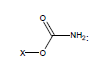
For example, the following constants which are calculated for carbamate species containing the carbamate functional group were determined to be σI = 0.45, σR = -0.34, σR- = -0.36, σR+ = -0.38, σPara = 0.10, σMeta = 0.32, σPhosph = 0.0238.
Secondary Algorithm
This is based on the following formula:
σR–G– = σ–G– + zI–G–∙σIR–
The accuracy of the σR–G– calculation is usually ±0.15–0.20. It is not as good as the first algorithm, but it can be used to calculate the σI, σ*, σR and σR- electronic constants for any possible substituents.
ACD/Sigma Database statistics
The typical accuracy of ACD/Sigma is ±0.05 in most cases. Sigma has been determined for aqueous solutions, at zero ionic strength and 25°C.
The accuracy of our calculation, and the extent of its applicability, is due to the large yet well-defined databases used. Following is an overview of two databases, from which
- certain parameters are derived for the electronic substituents in ACD/Sigma, and
- by which some calculation methods were evaluated and fine-tuned.
It is not necessary to know the database compounds or statistics in order to use the σ-calculator, but we believe that knowing the relative strengths of the composition of the databases which relate to the σ constant calculation will ultimately give you an idea of how well we can calculate σ-values for the type of chemical compounds you are interested in.
The database for ACD/Sigma contains over 850 substituents with over 3000 carefully derived experimental electronic constants. Included are the following constants:
| Sigma | Number in Database |
|---|---|
| σI | 592 |
| σ* (Taft) | 265 |
| σR | 453 |
| σR– | 157 |
| σR+ | 143 |
| σPara | 585 |
| σMeta | 431 |
| σPara– | 142 |
| σPara+ | 135 |
| σPhosph (P-Acids) | 68 |
| σOrtho (Benzoic acid) | 41 |
| σOrtho (Phenol) | 37 |
| σOrtho (Aniline) | 30 |
| σOrtho (Pyridine) | 48 |
The database was used to determine the parameters for the calculation of the electronic constants of substituents by primary and secondary algorithms. In cases when it was necessary to determine transmission parameters of bridges or electronic constants of substituents that were less well described in the database of electronic constants, the pKa database, containing about 16,000 compounds, was used.
Transmission Through Condensed Polyaromatic Systems
This is based on the modified Dewar-Grisdale method. The original Dewar-Grisdale method (Dewar M.J.S., Grisdale P.J., (1962). J. Am. Chem. Soc. 84, 3539) [12] can be used to calculate electronic transmission effects for only a very limited number of condensed polyaromatic systems. The improved ACD/Sigma method allows you to calculate these effects for virtually any polyaromatic systems.